Nous allons montrer comment se traduit cette simulation en un fichier XML que l'outil XMLlab va utiliser pour générer une simulation exécutée par Scilab. Le fichier XML sera montré sous sa forme textuelle.
Les lignes d'en-tête du fichier XML permettent toujours de lui associer la DTD de XMLlab, les lignes d'en-tête de la simulation qui suivent permettant de spécifier son titre, son auteur, des mots-clefs qui lui sont relatifs, ainsi qu'une image (ici des équations régissant la simulation) affichée en permanence en bas de la fenêtre de réglage des paramètres.
<?xml version="1.0" encoding="ISO-8859-1"?>
<!DOCTYPE simulation PUBLIC "-//UTC//DTD XMLlab V1.4//FR"
"http://www.xmllab.org/dtd/1.4/simulation.dtd">
<simulation>
<header>
<title lang="french">Cinétique de prédation de proies par des prédateurs</title>
<title lang="english">Kinetics of prey predation by predators</title>
<author>Pauss André, Mottelet Stéphane, UTC</author>
<keywords>simulation, scilab, xml, Lotka-Voltera</keywords>
<image href="Lotka-Voltera.gif" />
</header>
...Viennent ensuite des lignes définissant des notes multilingues, lesquelles sont affichées lors de la sélection de l'entrée de menu :
<notes lang="french">
<p>Cette simulation a pour objet d'illustrer l'équation de Lotka-Voltera qui décrit la dynamique des populations de proies et de prédateurs</p>
</notes>
<notes lang="english">
<p>This simulation aims to illustrate the kinetics of predation of preys by predators, with the Lotka-Voltera expression</p>
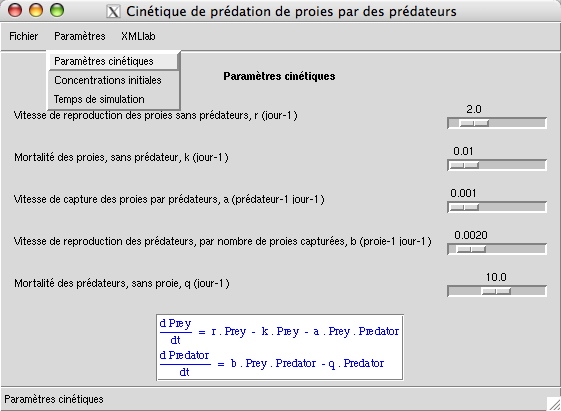
</notes>Les paramètres de la simulation sont groupés en plusieurs sections, chaque section donnant lieu à une entrée différente du menu de la simulation, comme le montre la figure suivante :
Le choix d'une entrée provoque alors l'affichage dans la fenêtre des paramètres correspondant. Les lignes suivantes introduisent et nomment les sections de paramètres :
<parameters>
<section>
<title lang="french">Paramètres cinétiques</title>
<title lang="english">Kinetic parameters</title>
...
</section>
<section>
<title lang="french">Concentrations initiales</title>
<title lang="english">Initial concentrations</title>
...
</section>
<section>
<title lang="french">Temps de simulation</title>
<title lang="english">Simulation duration</title>
...
</section>
</parameters>Nous allons maintenant décrire en détail la déclaration des
paramètres de chaque section, dont les lignes correspondantes figurent
après les balises multilingues <title> en question
:
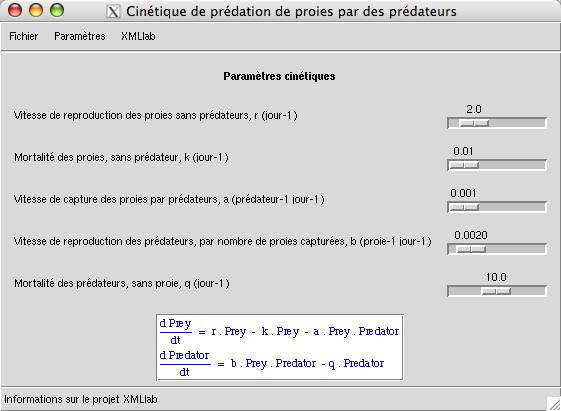
La saisie des paramètres de l'équation de Lotka-Voltera est effectuée dans la fenêtre illustrée par la figure suivante :
Cette section contient les paramètres suivants :
Vitesse
rde reproduction des proies sans prédateurs (j-1) :<scalar increment="0.1" label="r" max="10" min="0.5" unit="d-1" widget="slider"> <name lang="french"> Vitesse de reproduction des proies sans prédateurs, r (jour-1) </name> <name lang="english"> Growth rate of preys without predator, r (day-1) </name> <value>2</value> </scalar>Mortalité
kdes proies, sans prédateurs (j-1) :<scalar increment="0.01" label="k" max="3" min="0.0001" unit="d-1" widget="slider"> <name lang="french"> Mortalité des proies, sans prédateur, k (jour-1) </name> <name lang="english"> Mortality of prey, without predator, k (day-1) </name> <value>0.01</value> </scalar>Vitesse
ade capture des proies par prédateur (prédateur-1 . j-1) :<scalar increment="0.001" label="a" max="0.01" min="0.001" unit="" widget="slider"> <name lang="french"> Vitesse de capture des proies par prédateurs, a (prédateur-1 jour-1) </name> <name lang="english"> Predation rate of prey, per number of predator, a (predator-1 day-1) </name> <value>0.001</value> </scalar>Vitesse
bde reproduction des prédateurs, par nombre de proies capturées (proie-1 . j-1) :<scalar increment="0.0005" label="b" max="0.01" min="0.001" unit="" widget="slider"> <name lang="french"> Vitesse de reproduction des prédateurs, par nombre de proies capturées, b (proie-1 jour-1) </name> <name lang="english"> Growth rate of predators, per number of eaten prey, b (prey-1 day-1) </name> <value>0.002</value> </scalar>Mortalité
qdes prédateurs, sans proies (j-1) :<scalar increment="0.5" label="q" max="20" min="0.5" unit="d-1" widget="slider"> <name lang="french"> Mortalité des prédateurs, sans proie, q (jour-1) </name> <name lang="english"> Mortality of predators, without prey, q (day-1) </name> <value>10</value> </scalar>
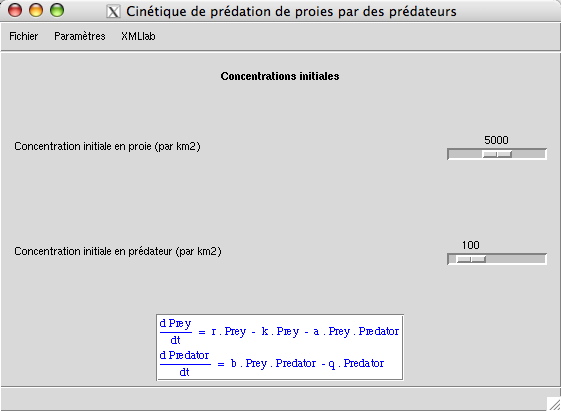
La saisie des concentrations initiales des proies et prédateurs par km2 est effectuée dans la fenêtre illustrée par la figure suivante :
Cette section contient les paramètres suivants :
Concentration initiale
Prey0en proie (par km2) :<scalar increment="1000" label="Prey0" max="10000" min="0" unit="" widget="slider"> <name lang="french"> Concentration initiale en proie (par km2) </name> <name lang="english"> Initial concentration of prey (per square km) </name> <value>5000</value> </scalar>Concentration initiale
Predator0en prédateur (par km2) :<scalar increment="50" label="Predator0" max="1000" min="1" unit="" widget="slider"> <name lang="french"> Concentration initiale en prédateur (par km2) </name> <name lang="english"> Initial concentration of predator (per square km) </name> <value>100</value> </scalar>
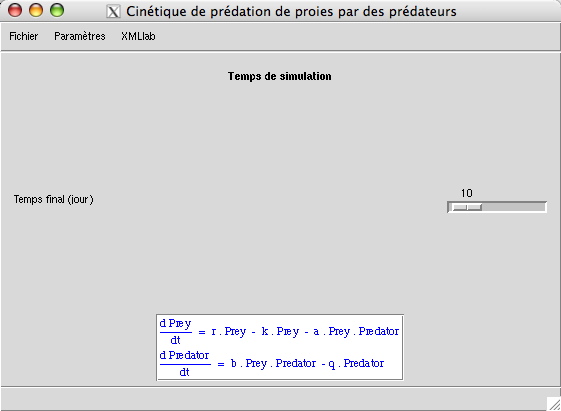
Sa saisie est effectuée dans la fenêtre illustrée par la figure suivante :
Cette section contient le seul paramètre suivant :
Temps final
final_time(j) :<scalar increment="1" label="final_time" max="200" min="0.001" unit="d" widget="slider"> <name lang="french">Temps final (jour)</name> <name lang="english">Final time (day)</name> <value>10</value> </scalar>
Cette section - qui suit la balise
</parameters> - permet de définir les équations à
résoudre, les courbes à calculer, ainsi que les domaines de valeurs
(1D ou 2D) que certaines variables doivent prendre. Ces différentes
définitions sont encadrées par les balises suivantes :
<compute> ... </compute>
En ce qui concerne notre simulation de cinétique de prédation de proies par des prédateurs, les éléments suivants y sont définis :
Ils sont utilisés pour la résolution de l'équation différentielle donnant l'évolution dans le temps du nombre de proies et de prédateurs :
<defdomain1d label="time" unit="d"> <name>Temps</name> <interval discretization="linear" steps="1000"> <initialvalue>0</initialvalue> <finalvalue>final_time</finalvalue> </interval> </defdomain1d>
Définition de l’élément ode
(ordinary differential equation)
regroupant la référence à la variable d'intégration
time et à son domaine de variation, ainsi que la
définition des états Prey et Predator,
avec pour chacun d'eux sa dérivée et sa valeur initiale :
<ode label="predation"> <refdomain1d ref="time" /> <states> <state label="Prey"> <name lang="french">Concentration en proie (km-2)</name> <name lang="french">Prey concentration (km-2)</name> <derivative>(r*Prey) - (k*Prey) - (a*Prey*Predator)</derivative> <initialcondition>Prey0</initialcondition> </state> <state label="Predator"> <name lang="french">Concentration en prédateur (km-2)</name> <name lang="french">Predator concentration (km-2)</name> <derivative>(b*Prey*Predator) - (q*Predator)</derivative> <initialcondition>Predator0</initialcondition> </state> </states> </ode>
Il s'agit de la courbe paramétrique x = Prey(t), y = Predator(t) qui permet de voir l'évolution conjointe du nombre de proies et du nombre de prédateurs :
<parametriccurve2d label="Prey_vs_predator"> <name lang="french">Portrait de phase</name> <name lang="english">Phase picture</name> <x1> <value>Prey</value> </x1> <x2> <value>Predator</value> </x2> </parametriccurve2d>
Cette section - qui suit la balise </compute>
- permet de définir les différentes fenêtres graphiques, un ensemble
de système d'axes pour chacune d'elle (les fenêtres pouvant alors se
diviser horizontalement ou verticalement pour les contenir), ainsi que
les courbes qui doivent être respectivement affichées dans chaque
système d'axe. Ces différentes définitions sont encadrées par les
balises suivantes :
<display> ... </display>
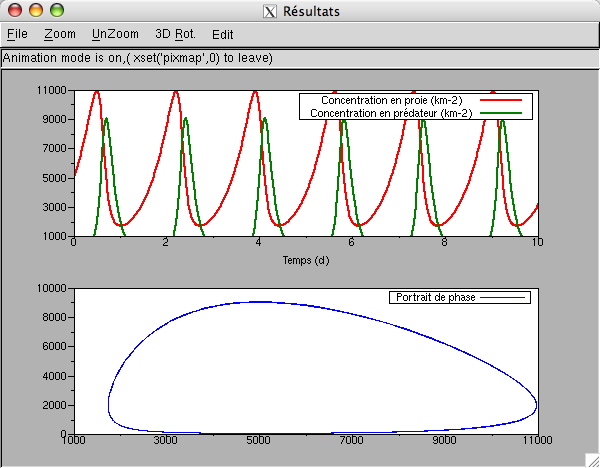
Dans notre cas, une seule fenêtre est divisée verticalement en deux systèmes d'axes cartésiens contenant les courbes suivantes :
Concentrations en proies et en prédateurs par km2 en fonction du temps.
Portrait de phase Proie contre Prédateur.
Le code correspondant est le suivant, les courbes logiques définies précédemment figurant en référence dans la définition des courbes à afficher :
courbe
Preyde l'évolution de la concentration des proies et courbePredatorde celle des prédateurs,portrait de phase :
Prey_vs_predator
<display>
<window splity="2">
<title lang="french">Résultats</title>
<title lang="english">Results</title>
<axis2d>
<drawcurve2d color="red" ref="Prey" thickness="2" />
<drawcurve2d color="green" ref="Predator" thickness="2" />
</axis2d>
<axis2d>
<drawcurve2d ref="Prey_vs_predator" />
</axis2d>
</window>
</display>Elle est accessible via l'entrée de menu pour cette simulation, grâce aux lignes suivantes spécifiant le fichier par défaut d'enregistrement, ainsi que la liste des paramètres et résultats à y enregistrer :
<save>
<file format="csv" href="essai.csv"
labels="r k a b q time Prey Predator" />
</save>Voici l'allure d'un exemple de fichier CSV obtenu, la balise
name de chaque paramètre ou résultat précédant sa
valeur :
"Vitesse de reproduction des proies sans prédateurs, r (jour-1) : ",2.000000, "Mortalité des proies, sans prédateur, k (jour-1) : ",0.001000, "Vitesse de capture des proies par prédateurs, a (prédateur-1 jour-1) : ",0.005000, "Vitesse de reproduction des prédateurs, par nombre de proies capturées, b (proie-1 jour-1) : ",0.002000, "Temps : ",0.000000,0.010010,...,10.000000, "Concentration en proie (km-2) : ",5000.000000,5096.003572,...,3358.727460, "Concentration en prédateur (km-2) : ",100.000000,100.095849,...,144.851043,