Nous allons montrer comment se traduit cette simulation en un fichier XML que l'outil XMLlab va utiliser pour générer une simulation exécutée par Scilab. Le fichier XML sera montré sous sa forme textuelle. Une fois de plus, seul les éléments de simulation non encore vus précédemment seront particulièrement détaillés.
Les lignes d'en-tête du fichier XML permettent toujours de lui associer la DTD de XMLlab, les lignes d'en-tête de la simulation qui suivent permettant de spécifier son titre, son auteur, ainsi que des mots-clefs qui lui sont relatifs.
<?xml version="1.0" encoding="ISO-8859-1"?>
<!DOCTYPE simulation PUBLIC "-//UTC//DTD XMLlab V1.4//FR" "http://www.xmllab.org/dtd/1.4/simulation.dtd">
<simulation>
<header>
<title lang="french">Simulation de l'équation de Poisson</title>
<title lang="english">Simulation of the Poisson equation</title>
<author email="stephane.mottelet@utc.fr">Stéphane Mottelet</author>
<date>03/2004</date>
<keywords lang="french">equation aux dérivées partielles, condensateur,
éléments finis</keywords>
<keywords lang="english">partial differential equation, condensator,
finite elements </keywords>
</header>
...Viennent ensuite des lignes définissant des notes multilingues, lesquelles sont affichées lors de la sélection de l'entrée de menu :
<notes lang="french">
<p>Cette simulation a pour but de montrer les possibilités de XMLlab en
termes de simulation d'équations aux dérivées partielles elliptiques.</p>
<p>On s'intéresse ici à un exemple simple où le bord extérieur du domaine
est mis à la masse, et où on impose deux tensions différentes sur les deux
frontières intérieures.</p>
</notes>
<notes lang="english">
<p>This simulation aims to show how XMLlab is able to deal with partial
differential equations.</p>
<p>Play with the sliders to change the mesh and see how the voltage on the
inner electrodes incluences the whole distribution.</p>
</notes>
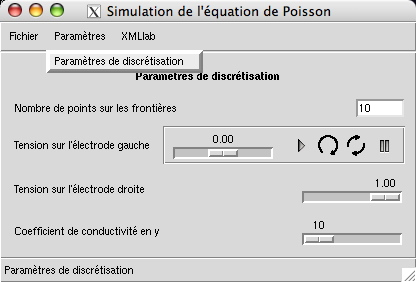
Les paramètres de cette simulation ne comportent qu'une section, donnant lieu à une unique entrée du menu de la simulation, comme le montre la figure suivante :
Les lignes suivantes introduisent et nomment l'unique section de paramètres :
<parameters>
<section>
<title lang="french">Paramètres de discrétisation</title>
<title lang="english">Discretization parameters</title>
...
</section>
</parameters>Nous allons maintenant décrire en détail la déclaration des
paramètres de cette section, dont les lignes correspondantes figurent
après les balises multilingues <title> :
Leur saisie est effectuée dans la fenêtre vue précédemment.
Cette section contient les paramètres suivants :
Nombre
nde points sur les frontières :<scalar increment="1" label="n" max="25" min="10"> <name lang="french">Nombre de points sur les frontières</name> <name lang="english">Number of points on the boundary</name> <notes lang="french"> <p>Ne pas dépasser n=20 si vous voulez garder</p> <p>une animation fluide.</p> </notes> <notes lang="english"> <p>Don't use more than n=20 points if you</p> <p>want to keep a smooth animation.</p> </notes> <value>10</value> </scalar>Tension
bsur l'électrode gauche, réglable par une glissière qui peut être animée automatiquement :<scalar increment="0.01" label="b" max="1" min="-1" widget="animate"> <name lang="french">Tension sur l'électrode gauche</name> <name lang="english">Voltage on the left electrode</name> <value>0</value> </scalar>L'utilisateur peut faire varier en continu la valeur du paramètre entre ses bornes définies, et selon le pas d'incrément spécifié :

Les 4 boutons situés en regard de la glissière permette respectivement de :
démarrer l'animation jusqu'à la valeur finale du paramètre,
de la démarrer en repartant depuis la valeur initiale quand la valeur finale est atteinte,
de la démarrer en repartant en sens inverse vers la valeur initiale quand la valeur finale est atteinte,
de mettre en pause l'animation.
Tension
asur l'électrode droite, réglable par une glissière :<scalar increment="0.01" label="a" max="1" min="-1" widget="slider"> <name lang="french">Tension sur l'électrode droite</name> <name lang="english">Voltage on the right electrode</name> <value>1</value> </scalar>Coefficient
dde conductivité en y, réglable par une glissière :<scalar increment="10" label="d" max="200" min="10" widget="slider"> <name lang="french">Coefficient de conductivité en y</name> <name lang="english">Conductivity coefficient in the y direction</name> <value>10</value> </scalar>
Cette section - qui suit la balise
</parameters> - permet de définir les équations à
résoudre, les courbes à calculer, ainsi que les domaines de valeurs
(1D ou 2D) que certaines variables doivent prendre. Ces différentes
définitions sont encadrées par les balises suivantes :
<compute> ... </compute>
En ce qui concerne notre simulation de l'équation de Poisson, les éléments suivants y sont définis :
Il s'agit de la variable qui sert à discrétiser Γ1 et Γ2 avec n points :
<defdomain1d label="thetain">
<interval discretization="linear" steps="n">
<initialvalue>0</initialvalue>
<finalvalue>2*%pi</finalvalue>
</interval>
</defdomain1d>On illustre également la possibilité d'utiliser des constantes
Scilab, ici %pi.
Il s'agit de la variable qui sert à discrétiser Γ0 avec 2n points :
<defdomain1d label="thetaout">
<interval discretization="linear" steps="2*n">
<initialvalue>0</initialvalue>
<finalvalue>2*%pi</finalvalue>
</interval>
</defdomain1d>Il a pour frontière Γ = Γ0 ∪
Γ1 ∪ Γ2. Sa
description (balise defdomain2d) est composée de la
description de ses frontières Γ0,
Γ1 et Γ2, chacune
d'elle étant décrite par une courbe paramétrique 2D (balise
parametriccurve2d) dépendant des variables
thetain et thetaout, la balise
refdomain1d indiquant la variable
(domain1d) en dépendance :
<defdomain2d dependencies="n" label="omega"> <border> <parametriccurve2d label="gamma_0"> <refdomain1d ref="thetaout"/> <x1> <value>cos(thetaout)</value> </x1> <x2> <value>sin(thetaout)</value> </x2> </parametriccurve2d> <parametriccurve2d label="gamma_1"> <refdomain1d ref="thetain"/> <x1> <value>0.4+0.2*cos(thetain)</value> </x1> <x2> <value>0.2*sin(-thetain)</value> </x2> </parametriccurve2d> <parametriccurve2d label="gamma_2"> <refdomain1d ref="thetain"/> <x1> <value>-0.4+0.25*cos(thetain)</value> </x1> <x2> <value>0.25*sin(-thetain)</value> </x2> </parametriccurve2d> </border> </defdomain2d>
L'attribut dependencies="n" permet d'indiquer que
la triangulation du domaine, qui est une opération coûteuse, ne doit
être effectuée que lorsqu'il change, donc quand n
change de valeur.
Elle est contenue dans le code qui suit, les correspondances étant les suivantes :
la matrice D (qui doit être une constante) correspond au contenu de la balise
diffusion,la fonction c(x, y) à la balise
proportional,f(x, y) à la balise
source,pour les conditions aux limites :
σ(x, y) et ξ(x, y) correspondent aux balises
sigmaetxi, absentes de cet exemple,g(x, y) à la balise
dirichlet
<stationary-pde label="pde1"> <refdomain2d ref="omega"/> <pdestate label="u"> <name lang="french">Tension</name> <name lang="english">Voltage</name> <inside dependencies="n d"> <diffusion>[10 0;0 d]</diffusion> <proportional>0</proportional> <source>0</source> </inside> <boundary> <condition bdy="gamma_0"> <dirichlet>0</dirichlet> </condition> <condition bdy="gamma_1"> <dirichlet>a</dirichlet> </condition> <condition bdy="gamma_2"> <dirichlet>b</dirichlet> </condition> </boundary> </pdestate> </stationary-pde>
Ici aussi, on utilise l’attribut dependencies de
la balise inside pour ne calculer que ce qui est
nécessaire lorsque les paramètres changent. Ainsi, l'assemblage du
problème dans le domaine n'est refait que si n ou
d changent, permettant de faire varier les conditions
aux limites sans refaire un gros calcul inutile.
Cette section - qui suit la balise </compute>
- permet de définir les différentes fenêtres graphiques, un ensemble
de système d'axes pour chacune d'elle (les fenêtres pouvant alors se
diviser horizontalement ou verticalement pour les contenir), ainsi que
les courbes qui doivent être respectivement affichées dans chaque
système d'axe. Ces différentes définitions sont encadrées par les
balises suivantes :
<display> ... </display>
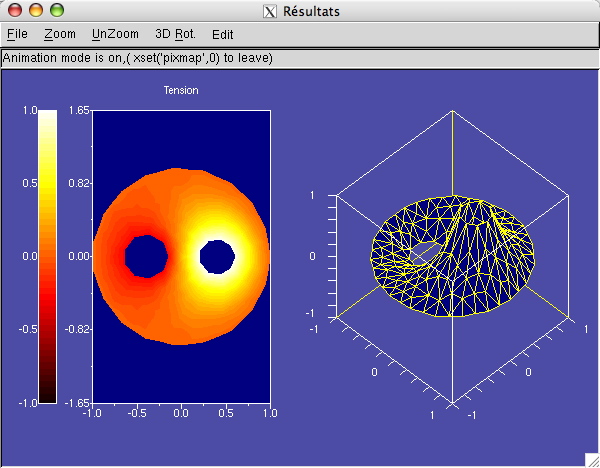
Dans notre cas, une seule fenêtre est divisée horizontalement en deux systèmes d'axes contenant des représentations différentes de la surface u(x,y), (x,y) ∈ Ω :
Représentation à plat en 2D (x,y), les variations de u étant figurées par des variations de couleurs.
Représentation en 3D isométrique de la surface en fil de fer.
Le code correspondant est le suivant, les courbes logiques définies précédemment figurant en référence dans la définition des courbes à afficher :
représentation de
uà plat en 2D : les attributscminetcmaxde la baliseaxis2dindiquent la plage de variation deu,représentation en 3D surfacique : l'attribut
mode="wireframe"indique qu'une représentation en fil de fer est désirée,
<display background="blue">
<window colormap="hot" splitx="2">
<title lang="french">Résultats</title>
<title lang="english">Results</title>
<axis2d cmax="1" cmin="-1" colorbar="on" iso="yes">
<drawsurface ref="u" shading="interp"/>
</axis2d>
<axis3d xmin="-1" xmax="1" ymin="-1" ymax="1" zmin="-1" zmax="1">
<drawsurface mode="wireframe" ref="u"/>
</axis3d>
</window>
</display>