Table des matières
Cet exemple, qui va être décrit complètement, correspond au fichier
Physics/gravitation.xml du sous-répertoire
examples du répertoire d'installation de
XMLlab.
Il s'agit de simuler le mouvement de deux ou plusieurs corps soumis à leurs attractions gravitationnelles mutuelles.
Dans le cas de deux corps, le problème a été résolu analytiquement, et l’on sait bien que les trajectoires obtenues sont des coniques ayant pour foyer le centre de gravité du système formé par ces deux corps. Le problème des trois corps a toujours échappé aux mécaniciens, car il n’est plus possible dans ce cas de trouver de solution analytique (pour plus de trois corps non plus, bien sûr). Les problèmes à plus de deux corps ont été très vite envisagés car on s’est très vite rendu compte que les trajectoires des planètes autour du soleil ne sont pas celles prévues par la théorie simplifiée consistant à considérer autant de problèmes à deux corps qu’il y a de planètes en orbite : les planètes s’influencent mutuellement, de façon faible par rapport à la force de gravitation exercée par le Soleil, mais suffisamment pour que les trajectoires à long terme soient modifiées.
Il a donc fallu très vite savoir calculer avec précision ces trajectoires pour constituer ce qu’on appelle des éphémérides, véritables tables où l’on peut lire la position de divers corps célestes à des dates futures. Les positions de ces corps vérifient des équations différentielles, et les techniques d’approximation sont les mêmes que celles utilisées pour la simulation du pendule (cf. document Prise en main XMLlab).
Nous allons rapidement décrire comment mettre en oeuvre la simulation d’un problème à deux corps. D’abord, quelques rappels sont nécessaires : considérons deux corps sphériques de centres u1 = (x1, y1) et u2 = (x2, y2), de masses respectives m1 et m2. La force de gravitation exercée par le corps 2 sur le corps 1 est égale à
où G est la constante de gravitation universelle. La force de gravitation exercée par le corps 1 sur le corps 2 est égale à son opposé, soit
F12 = −F21.
Si nous désirons simuler le mouvement de ces deux corps en fonction d’une configuration initiale de position et de vitesse, nous devons écrire les équations de la dynamique, qui donnent
si on note v1, v2 les vitesses, et
Ici le corps 1 est la Terre et le corps 2 la Lune.
m1 = 5,975e24 ; m2 = 7,35e22 ; G = 6,67e-11 ; La distance moyenne Terre-Lune est de dTL = 3, 84402e8 m et la période de rotation est à peu près de T = 27,55 jours. Nous choisissons donc comme positions initiales
et comme vitesses initiales
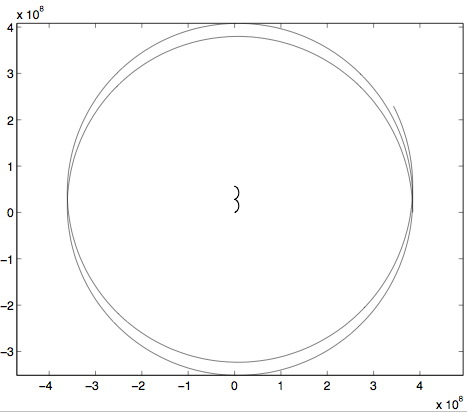
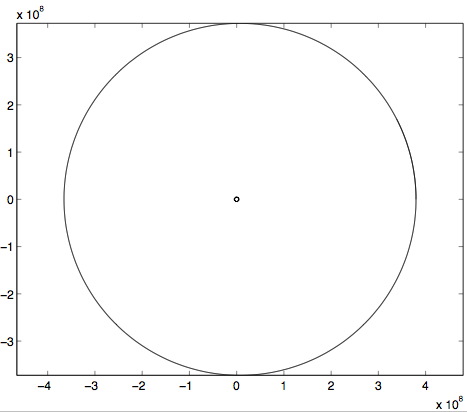
La Figure 5.1, « Trajectoires du système Terre-Lune » montre les deux trajectoires obtenues (on reconnaîtra aisément la trajectoire de la Terre), qui peuvent sembler bizarres mais il ne faut pas oublier qu’il faut se ramener au centre de gravité pour y voir plus clair. Il suffit de calculer la position du centre de gravité à chaque instant et de soustraire ses coordonnées à celles de la Lune et de la Terre. Cela donne la Figure 5.2, « Trajectoires du système Terre-Lune dans le repère lié au centre de gravité », qui est plus familière. On notera que la Terre subit de façon évidente l’influence de la Lune.