Nous allons montrer comment se traduit cette simulation en un fichier XML que l'outil XMLlab va utiliser pour générer une simulation exécutée par Scilab. Le fichier XML sera montré sous sa forme textuelle. Cet exemple sera traité d'une manière analogue à l'exemple précédent.
Les lignes d'en-tête du fichier XML permettent toujours de lui associer la DTD de XMLlab, les lignes d'en-tête de la simulation qui suivent permettant de spécifier son titre, son auteur, ainsi que des mots-clefs qui lui sont relatifs.
<?xml version="1.0" encoding="ISO-8859-1"?>
<!DOCTYPE simulation PUBLIC "-//UTC//DTD XMLlab V1.4//FR" "http://www.xmllab.org/dtd/1.4/simulation.dtd">
<simulation>
<header>
<title>Système Terre-Lune</title>
<author>Please set author's name</author>
<keywords>simulation,scilab,xml</keywords>
</header>
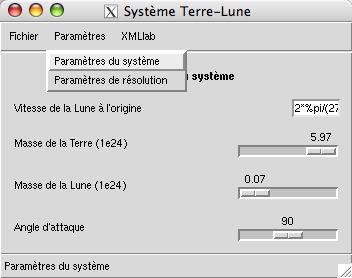
...Les paramètres de la simulation sont groupés en plusieurs sections, chaque section donnant lieu à une entrée différente du menu de la simulation, comme le montre la figure suivante :
Le choix d'une entrée provoque alors l'affichage dans la fenêtre des paramètres correspondant. Les lignes suivantes introduisent et nomment les sections de paramètres :
<parameters>
<section>
<title>Paramètres du système</title>
...
</section>
<section>
<title>Paramètres de résolution</title>
...
</section>
</parameters>Nous allons maintenant décrire en détail la déclaration des
paramètres de chaque section, dont les lignes correspondantes figurent
après les balises multilingues <title> en question
:
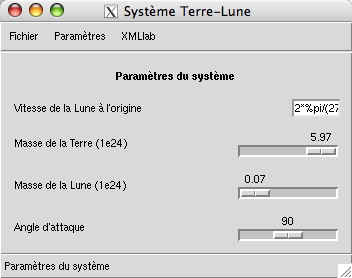
Leur saisie est effectuée dans la fenêtre illustrée par la figure suivante :
Cette section contient les paramètres suivants :
Vitesse
vL0de la lune à l'origine :<scalar label="vL0" unit="ms^-1"> <name>Vitesse de la Lune à l'origine</name> <value>2*%pi/(27.55*24*3600)*3.84402e8</value> </scalar>Masse
mTde la terre / 1e24 :<scalar label="mT" unit="m" widget="slider" min="4" max="5.975" increment="0.01"> <name>Masse de la Terre (1e24)</name> <value>5.975</value> </scalar>Masse
mLde la lune / 1e24 :<scalar label="mL" unit="m" widget="slider" min="0.0735" max="5.975" increment="0.01"> <name>Masse de la Lune (1e24)</name> <value>0.0735</value> </scalar>Angle
thetad'attaque entre le vecteur lune-terre et le vecteur vitesse initial de la lune (thetadétermine la direction de v2(0)) :<scalar label="theta" unit="deg" widget="slider" min="1" max="179" increment="1"> <name>Angle d'attaque</name> <value>90</value> </scalar>
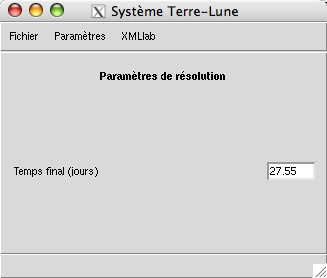
Leur saisie est effectuée dans la fenêtre illustrée par la figure suivante :
Cette section contient l'unique paramètre suivant :
Temps
jffinal (jours) : il s'agit de la durée de la simulation, la valeur proposée étant la période de rotation T de la lune autour de la terre.jfest utilisé pour calculer la borne supérieure de l'intervalle de discrétisation intervenant dans la résolution de l'équation différentielle donnant les mouvements de la terre et de la lune :<scalar label="jf" unit="d"> <name>Temps final (jours)</name> <value>27.55</value> </scalar>
Cette section - qui suit la balise
</parameters> - permet de définir les équations à
résoudre, les courbes à calculer, ainsi que les domaines de valeurs
(1D ou 2D) que certaines variables doivent prendre. Ces différentes
définitions sont encadrées par les balises suivantes :
<compute> ... </compute>
En ce qui concerne notre simulation de la mécanique céleste, les éléments suivants y sont définis :
Il s'agit de la variable d'intégration utilisée pour la résolution de notre équation différentielle, l'intervalle de discrétisation étant découpé en 1000 pas :
<defdomain1d label="t" unit="s"> <name>Temps</name> <interval discretization="linear" steps="1000"> <initialvalue>0</initialvalue> <finalvalue>jf*24*3600</finalvalue> </interval> </defdomain1d>
Définition de l’élément ode (ordinary
differential equation) regroupant :
la référence à la variable d'intégration
tet à son domaine de variation,la définition des états
xTetvT(position et vitesse de la terre) d'une part,xLetvL(position et vitesse de la lune) d'autre part, avec pour chacun d'eux sa dérivée et sa valeur initiale ; il est à noter que chacun de ces états est un vecteur possédant deux composantes x et y (size="2"),la sortie
xGdonnant la position du centre de gravité du système Terre-Lune.
<ode label="terre_lune"> <refdomain1d ref="t"/> <states> <variable label="r3">norm(xT-xL)^3</variable> <state label="xT" size="2"> <name>Position de la terre</name> <derivative>vT</derivative> <initialcondition>[0;0]</initialcondition> </state> <state label="vT" size="2"> <name>Vitesse de la terre</name> <derivative>6.67e-11*mL*1e24*(xL-xT)/r3</derivative> <initialcondition>[0;0]</initialcondition> </state> <state label="xL" size="2"> <name>Position de la Lune</name> <derivative>vL</derivative> <initialcondition>[3.84402e8;0]</initialcondition> </state> <state label="vL" size="2"> <name>Vitesse de la Lune</name> <derivative>6.67e-11*mT*1e24*(xT-xL)/r3</derivative> <initialcondition> vL0*[cos(%pi*theta/180);sin(%pi*theta/180)] </initialcondition> </state> </states> <outputs> <output label="xG"> <name>Centre de gravité</name> <value>(xL*mL+xT*mT)/(mL+mT)</value> </output> </outputs> </ode>
Il s'agit de la position de la terre relativement au centre de gravité du système Terre-Lune :
<parametriccurve2d label="traj_terre"> <name>Terre</name> <refdomain1d ref="t"/> <x1> <value>xT(:,1)-xG(:,1)</value> </x1> <x2> <value>xT(:,2)-xG(:,2)</value> </x2> </parametriccurve2d>
Il s'agit de la position de la lune relativement au centre de gravité du système Terre-Lune :
<parametriccurve2d label="traj_lune"> <name>Lune</name> <refdomain1d ref="t"/> <x1> <value>xL(:,1)-xG(:,1)</value> </x1> <x2> <value>xL(:,2)-xG(:,2)</value> </x2> </parametriccurve2d>
Cette section - qui suit la balise </compute>
- permet de définir les différentes fenêtres graphiques, un ensemble
de système d'axes pour chacune d'elle (les fenêtres pouvant alors se
diviser horizontalement ou verticalement pour les contenir), ainsi que
les courbes qui doivent être respectivement affichées dans chaque
système d'axe. Ces différentes définitions sont encadrées par les
balises suivantes :
<display> ... </display>
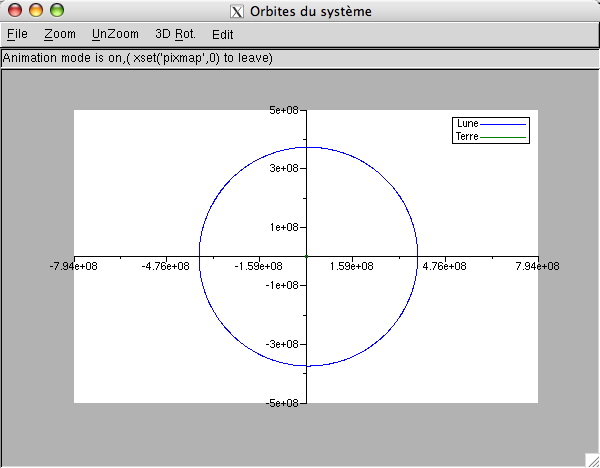
Dans notre cas, une seule fenêtre contient un système d'axe cartésien contenant les courbes des trajectoires de la terre et de la lune :
Le code correspondant est le suivant, les courbes logiques définies précédemment figurant en référence dans la définition des courbes à afficher :
<display>
<window>
<title>Orbites du système</title>
<axis2d position="origin" iso="yes"
xmin="-5e8" ymin="-5e8" xmax="5e8" ymax="5e8">
<drawcurve2d ref="traj_lune"/>
<drawcurve2d ref="traj_terre" color="green"/>
</axis2d>
</window>
</display>